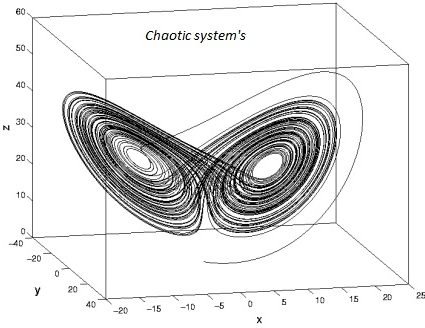
معرفی سیستم های آشوبناک

نمــاي ليــاپانوف (Lyapunov exponent): نماي لياپانوف توسط « ليــاپانوف» رياضيدان روسي در سال 1892 ميلادي براي كنتــرل پايداري معادلات ديفرانسيــل غيرخطي مورد استفاده قرار گرفت. اين روش امكان مطالعه پايداري معادلات ديفرانسيل را بدون حل آنها امكانپذيــر مي ­سازد. با توجه به اين كه براي مطالعه يك سيستم ديناميكي غيرخطي ضروري است كه آن را توسط نگاشت ها مورد مطالعه قرار داد، به توصيف نماي لياپانوف كه مطالعه رفتار سيستم ها توسط نگاشت را به صورت عددي ميسر مي­ سازد، پرداخته مي­ شود.

براي اين كه يك سيستم را آشوبناک بناميم بايد نشان دهيم كه سيستم وابستگي حساس به شرايط اوليه دارد يعني اين كه دو مسير كه خيلي نزديك به هم شروع مي ­شوند خيلي سريع به طور نمايي از هم واگرا شده و آينده متفاوتي پيدا مي ­كنند. گفته شد كه وابستگي حساس معادلات ديفرانسيل بي ­نظم با نماي لياپانوف تعريف مي ­گردد، اكنون اين تعريف را براي نگاشت هاي يك بعدي بسط می دهیم.

فرض مي ­كنيم x0 نقطه­ اي در لحظه t در روي يك مسير و x0 + d0 نقطه­ اي نزديك به آن در روي مسير ديگر مي­ باشد كه d0 بي­نهايت كوچك بوده و معرف ميزان اوليه جدايي اين دو نقطه است. اگر ميزان جدايي اين دو نقطه بعد از n تكرار(Iteration) توسط d^n نمايش شود و رابطه­ اي به صورت |d^0|exp(λ^n) = |d^n| مابين اين دو نقطه برقرار كنيم. در اين صورت مي توان λ را به عنوان نماي لياپانوف معرفي كرد.

1. با مثبت شدن مقدار λ فاصله دو نقطه در فضاي فاز با نگاشت هاي مكرر، به صورت نمايي افزايش مي­ يابد، يعني سيستم به سمت آشوبناك شدن ميل پيدا مي ­كند.
2. با منفي شدن مقدار λ مي ­توان دريافت كه نقطه ثابت، رفتار پايداري را از خود نشان مي ­دهد، يعني سيستم به حالت پايدار مي­رسد.
3. شرط λ = 0 نيز معرف حالت حاشيه ­اي است.

با استناد به رابطه بالا و نيز با لگاريتم گرفتن و انجام يك سري اعمال رياضي، نماي لياپانوف در نهايت به صورت رابطه زير به دست مي آيد:

l = (1/n) S Ln |f ‘(xi)|

عبارت به دست آمده زمانی که مخرج کسر به سمت صفر میل کند دارای حدی است که آن را نمای لیاپانوف می نامند.

در این نوشته سعی کردیم تا مختصرا به “معرفی سیستم های آشوبناک” بپردازیم.

#اختصاصی مهندسی کنترل