
مسئله کنترل LQR
یکی از مباحث پایه ای و مهم که در حوزه کنترل بهینه خطی یا Linear Optimal Control بررسی و مطالعه می شود، طراحی و پیاده سازی “رگولاتور خطی درجه دو” یا Linear Quadratic Regulator و یا به اختصار LQR است. این استراتژی، یکی از رویکردهای مهم و پایه ای در کنترل بهینه است و تعمیم آن در سیستم های غیرخطی، استفاده ها و کاربردهای فراوان عملی و صنعتی دارد. در این مسأله دهدف تنظيم (Regulation) خروجی یک سیستم خطی (Linear) است به نحوی که یک تابع هزینه درجه دو (Quadratic) مینیمایز شود. در LQR، قانون کنترل را به گونهای محاسبه میکنیم که تابع هزینه درجه دوم زیر کمینه شود.
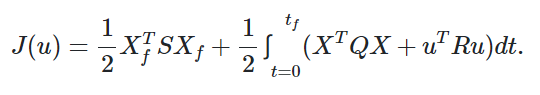
که در آن، Q یک ماتریس معین نیمهمثبت است و هزینه یا ارزش انحراف متغیرها از صفر را نشان میدهد، R یک ماتریس معین مثبت است و هزینه کنترل را نشان میدهد، و S یک ماتریس معین مثبت است که خطا از مقدار مطلوب نهایی (در اینجا، صفر) را جریمه میکند. ماتریسهای Q و R به صورت یک ماتریس قطری انتخاب میشوند. مقادیر بزرگ Q خطای مسیر و مقادیر بزرگ R کنترل را جریمه میکنند. بنابراین، استفاده از این فرمولبندی، کار طراح کنترل را برای تشخیص قطبهای سیستم آسان کرده و تمرکز او را به تنظیم وزنهای مربوط به هزینه کنترل و خطای ردیابی محدود میکند. یک فرایند طراحی کنترل معمولی با تغییر وزنهای خطای ردیابی و هزینه یا تلاش کنترلی سر و کار دارد تا پاسخ مناسب به دست آید.
بیان مسئله:
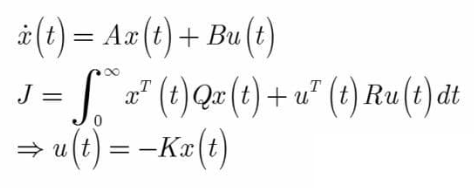
گین K را از حل معادله جبری ریکاتی می توان محاسبه کرد و در نرم افزار MATLAB از دستور lqr برای محاسبه گین K استفاده می شود.
![]()
در این نوشته سعی کردیم تا مختصرا برای شما عزیزان به معرفی “مسئله کنترل LQR” بپردازیم.

